Historias de la Ciencia

El libro que hoy quiero comentaros tiene una forma curiosa de enfocar la historia de las matemáticas: aprovecha el alfabeto para dar un repaso tanto de los conceptos como de la vida de muchos de los grandes, asociando a cada letra un personaje o algún hecho matemático destacable en la historia. Mezcla trozos de biografías con demostraciones matemáticas de todo tipo. Para quien no tenga suficiente soltura matemática recomiendo que haga un esfuerzo: valdrá la pena. Aun así, si no se desea hacer, dichos pasajes se pueden obviar perfectamente.

Por su forma e idea de divulgación de las matemáticas, me ha recordado mucho a otro titulado “Más allá de los números” de John Allen Paulos, pero este me ha gustado mucho más. Por supuesto, nunca hemos de menospreciar a Paulos, aunque de este último autor recomendaría antes “El hombre anumérico” (en mi opinión, el mejor libro de Paulos, aunque hay que recordar que tiene bastantes más).

Pero volvamos con el libro de hoy. Es relativamente largo, de unas 400 páginas pero de tamaño pequeño, letra mediana y muchísimas ilustraciones. Os hago un breve resumen sin olvidar que dejo en el tintero muchos más temas de los que trata.

Los números primos siempre han sido la atracción de los matemáticos. Marin Mersenne estaba intrigado por aquellos que tenían la forma 2^p-1, siendo p un número primo. Los resultantes son obviamente impares, pero lo curioso es que muchos de ellos también son primos. A aquellos que tienen esa forma se les llama números primos de Mersenne. Pero la cosa no está del todo clara. Se cumple para 2, 3, 5 y 7:

2² – 1 = 3
2³ – 1 = 7
2⁵ – 1 = 31
2⁷ – 1 = 127

Y se acaba aquí. Si tomamos el 11 tenemos que 2¹¹ – 1 = 2.047 que es también el producto de 23 x 89. Mersenne sabía perfectamente que, aunque el exponente del 2 fuera un número primo, no era garantía suficiente para que el resultado de 2^p – 1 también lo fuera. Conjeturó que sólo los números primos para los que se cumplía la fórmula eran 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 y 257. Pero, ¡ay!, se le pasó que 2⁶¹ – 1 también era primo y, por otro lado, 2⁶⁷ – 1 no es primo. Este último caso fue indicado por Edouard Lucas en 1876. Demostró de forma indirecta que debía tener divisores pero sin llegar a mostrarlos.

En 1903 el problema quedó resuelto de una forma fascinante. Había una reunión de la American Mathematical Society. Entre los conferenciantes programados figuraba Frank Nelson Cole. Cuando le tocó el turno, se adelantó al extremo de la sala. En completo silencio, multiplicó 2 por 2, 67 veces y le restó cuidadosamente 1, obteniendo la enorme cifra de 147.573.952.588.676.412.927. Los que, más que escuchar, observaban, vieron asombrados cómo Cole iba al otro lado de la pizarra y escribía a continuación 193.707.721 x 761.838.257.287 realizándola y obteniendo el mismo resultado. Entre que los asistentes quedaron sin habla y que el conferenciante se fue a su asiento sin haber pronunciado una sola palabra, ya podéis imaginar la emoción del momento. Todos sabían que era histórico. De pronto, la sala prorrumpió en aplausos. Le hicieron una larguísima ovación. Más tarde, Cole confesaría que le llevó más de dos décadas (según el libro y en castellano, en inglés dijo exactamente “three years of Sundays”).

Cita una anécdota de Erdös, del que hace poco os hablé. A la edad de 21 años, después de haber asombrado a la comunidad matemática con una demostración mucho más sencilla de aquel teorema que decía que entre un número entero y su doble hay, al menos, un número primo, untó por primera vez en su vida un trozo de pan con mantequilla, cosa que recordó más tarde:

Acababa de marcharme a Inglaterra para estudiar. A la hora del té, pusieron pan. Pasé también un gran apuro al tener que admitir que nunca había untado mantequilla. Lo intenté. No fue tan difícil.

Por supuesto, que Erdös no supiera untar pan con mantequilla o atarse los zapatos no le quita mérito.

Habla de un par de componentes de la pintoresca familia Bernoulli. Jakob hizo una de las primeras obras maestras en teoría de la probabilidad, la llamada Ars Conjectandi. Durante 30 años fue uno de los primeros matemáticos del mundo. No obstante, tenía una personalidad hiriente, un gran orgullo y una marcada tendencia a minusvalorar los esfuerzos de personas menos dotadas. Aun así, hay que decir a su favor que fue uno de los principales responsables en la popularización del cálculo recién inventado de Leibnitz.

Pues bien, resulta que le enseñó matemáticas a su hermano menor, Johann, quien se convirtió en un durísimo competidor. De hecho, hubo una fuerte rivalidad por la supremacía matemática. Mientras Johann no disimulaba su alegría cuando resolvió un problema con el que no había podido Jakob, éste último le llamaba “discípulo” intencionadamente. Una disputa famosa se produjo por una curva llamada catenaria, (aquella que se produce al colgar una cuerda sujeta por dos puntos). Mientras Jakob no pudo resolverlo, su hermano Johann sí y corrió a decírselo dejándolo perplejo. Jakob contraatacó con el problema isoperimétrico. Esto es: entre todas las curvas del mismo perímetro, dar la que encierra mayor área. Por ejemplo, en unidades arbitrarias, un rectángulo de lados 1 y 9 tiene un perímetro de 20 y el área sería de 9; pero un cuadrado con el mismo perímetro (de 5×5) tendrá un área de 25 (en gaussianos han tratado el tema hace poco).

Pero volvamos con Jakob. Este problema le obligó a vérselas con una ecuación diferencial de tercer orden (una ecuación con terceras derivadas). Con ello abrió el camino de una rama de las matemáticas que hoy llamamos cálculo de variaciones. Johann discrepó y dijo que era, en realidad, de segundo orden y no tercero. Aquí tenía razón Jakob; pero no pudo apenas reír porque murió. Para editar los trabajos de Jakob, sugirieron a su hermano Johann, pero imaginad cómo estaba el pique familiar que la viuda de Jakob lo impidió. No obstante, aunque en este libro no se hable mucho más de ellos, la familia Bernoulli tiene mucha más miga y tendré que explicarla en otra historia.

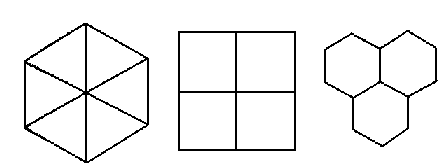
También da la demostración de que sólo hay tres maneras de disponer polígonos idénticos alrededor de un vértice común sin que haya intersticios: 6 triángulos equiláteros, 4 cuadrados y 3 hexágonos regulares (este último caso es el que utilizan las abejas).

Habla también del intento de patentar el número PI que ya os expliqué; pero da algún detalle más como que dos brillantes y excéntricos hermanos llamados David y Gregory Chudnovsky, nacidos en Kiev, desarrollaron el algoritmo para calcular PI que hoy utiliza el programa Mathematica. Ellos quisieron calcularlo con una precisión de hasta dos mil millones de dígitos en una computadora construida por ellos a base de piezas pedidas por correo en su apartamento de Manhattan. Su proyecto llenó mesas y mesas con las piezas del computador y salones y pasillos con todo tipo de cables. El calor generado por todo el follón elevó el apartamento hasta unas temperaturas infernales. Pero lo hicieron.

Habla del problema que planteó en su día Gerolamo Cardano, quien sostenía que no existían dos números reales que sumaran 10 y cuyo producto fuera 40 … y tenía razón.

Habla de Euler, quien se interesó por el cálculo, el álgebra, la geometría; que dio luz a nuevas ramas de las matemáticas como la teoría de curvas, topología combinatoria, cálculo de variaciones, etc., que se interesó por la óptica, mecánica, electricidad, acústica … hasta la estructura subyacente de la música. Decían de este último trabajo que contenía demasiada geometría para los músicos y demasiada música para los geómetras. Fue de lo más prolífico: hoy día existen unos 70 volúmenes; cada uno de ellos tiene unas 500 páginas y pesa unos 2 kg; así que tenemos de él unos 140 kg de sabiduría en sus libros … Distinguió entre funciones algebraicas y trascendentes y entre funciones elementales y superiores, desarrolló las coordenadas polares y la representación paramétrica de las curvas. Hasta le dieron un premio por determinar la óptima colocación de los mástiles en un barco de pasajeros. Por si fuera poco, era una persona sencilla, sin pretensiones. Me descubro ante Euler.

El autor aprovecha a este personaje para poner sobre el tapete un tema del que ya hemos hablado muchas veces: que muchas de las personas que apenas han oído hablar de él no tienen problema en conocer a personajes tan dispares como Pierre Auguste-Renoir, Johannes Brahams o Walter Scott. Pero advierte que no es comparable Renoir con Rembrandt, Brahams con Bach o Walter Scott con Shakespeare. Pues bien, Euler es el Shakespeare de las matemáticas y es una pena que no sea tan conocido como él.

Habla de Fermat, quien nunca publicó un tratado. Si no hubiera tenido un carácter tan cerrado, en lugar de plano cartesiano, hoy hablaríamos de “plano fermitiano”. Por supuesto, no deja de nombrar el último Teorema de Fermat y algunas de las divertidas anécdotas que nos han obsequiado las mentes más agudas de la historia a través de él. Cuando el libro entraba en prensa, Andrew Wiles estaba a punto de sorprender al mundo con la demostración del mismo. Algún día, si queréis, os puedo hablar de ello comentando el libro “El Último Teorema de Fermat”, de Simon Sigh, donde hace un maravilloso relato de su historia.

Habla también del teorema de Pitágoras y de que un profesor de principios del siglo XX llamado Elisha Scott Loomis reunió y publicó 367 demostraciones del mismo. Dice que hay evidencias que los chinos demostraron ese teorema antes de Pitágoras, pero lo más divertido es que hay quienes dudan que utilizara ese método para demostrarlo, que hay quienes dudan que Pitágoras lo demostrara y que hay, incluso, quienes dudan que Pitágoras haya existido. En fin, la conclusión es que no sabemos nada de nada.

Explica posibles trampas en que pueden caer los matemáticos como que no bastan unos cuantos casos para confirmar una suposición. Los matemáticos utilizan argumentaciones muy convincentes para demostrar que “algo no existe”. Muy parecido al dragón en el garaje: suponemos que existe, lo desarrollamos de una forma fría y lógica y llegamos a una contradicción. Que un contraejemplo es un arma demoledora que invalida una posible hipótesis; el problema es encontrarlo. Y, creedme, no es nada trivial muchas veces. Por ejemplo, Euler conjeturó que hacía falta sumar, al menos, n potencias para obtener una potencia de orden n. Por ejemplo:

Para n=2 tenemos 3² + 4² = 5²
Para n=3 tenemos 3³ + 4³ + 5³ = 6³

O sea, tantos sumandos como valor tenga el exponente. Así quedó el asunto en 1778. Los que creyeron en Euler no pudieron demostrarlo. En 1966 los matemáticos Leon Lander y Thomas Parkin descubrieron que:

27⁵ + 84⁵ +110⁵ + 133⁵ = 144⁵

Ese contraejemplo invalidaba la conjetura. Sí, ya sé, Euler se equivocó, pero no seré yo quien se lo recrimine. Y es que las demostraciones matemáticas son totalmente diferentes de cualquier otra ciencia. Un químico que deja caer 50.000 trozos de sodio metálico en 50.000 vasos de precipitado con agua y observa 50.000 explosiones, extrae una conclusión diciendo que ha demostrado algo. Un matemático que hace 50.000 quebrados y encuentra que ninguno de ellos es igual a raíz de 2 concluye que está en el mismo punto que antes.

Resumiendo: los matemáticos no sólo buscan que una prueba esté más allá de toda duda razonable, sino más allá de toda duda.

También habla del sentido del humor y la forma de ser de los matemáticos. En vez de vestir normal y como todo el mundo, se ponen camisetas con inscripciones de alguna movida matemática (los físicos, en ese aspecto, no les van muy lejos).

Que los que escriben tiras cómicas se equivocan: los matemáticos no llevan bata blanca y que es más probable ver llevar una bata blanca a un luchador de sumo que no a un matemático. Que abundan los barbudos matemáticos: afeitarse es ilógico y que el único sitio donde podremos encontrar más barbas que en un congreso de matemáticos es en un congreso de Santa Claus.

Distingue entre dos tipos de humor matemático: el “bajo” y el “alto”. El bajo es la confusión pretendida de la terminología matemática como homotopía o difeomorfismo; aunque algunas palabras se han colado al lenguaje habitual como matriz o parámetro. El humor matemático bajo es, por ejemplo, llamar a una reunión de colegas “grupo finito”.

El humor alto es mucho más sutil y entra cuando los engranajes se salen totalmente de su sitio. Un ejemplo es lo que Pólya escribía: “¿Qué es un filósofo? Uno que lo sabe todo y nada más” o Pauli (aunque era físico, pero igual de retorcido) cuando decía “Tan joven y tan desconocido” (en ciencias puras se dice que si no has destacado de joven, de mayor ya no sirves: tienes demasiados prejuicios). Cita varias más pero que tienen que ver con un doble sentido en inglés.

Explica también que los matemáticos son despreciados por el resto de los mortales (no es el caso de un servidor que aunque siempre diga que están locos es por pura envidia), en el aspecto que muchos afirman que odian las matemáticas o que les asustan o ambas cosas. ¿Acaso fueron mordidos de niños por un matemático? Imaginad una conversación del tipo:

Profesor: ¿Quiénes fueron los Reyes Católicos?
Alumno: Lo siento, yo nunca pude estudiar historia.

Si un matemático se jactara de no haber leído nunca poesía sería inmediatamente tachado de ignorante, pero si un poeta admite ser un analfabeto matemático lo lleva con orgullo. ¿A que no parece equitativo?

También nos recuerda que Gauss, aunque reconoció el patrón, no pudo demostrar el Teorema de los Números Primos ni nadie durante los cien años siguientes hasta que dos lumbreras llamados Jacques Hadamard y C. J. de la Vallee Pousin lo lograron utilizando técnicas que se escapan a muchos de nosotros.

Que, a veces, las innovaciones en el campo matemático son terriblemente mal acogidas. Muchos se opusieron violentamente a la extensión de números enteros a los negativos. Michael Stifel (1487-1567) decía de ellos “numeri absurdi” y Gerolamo Cardano decía despectivamente “numeri ficti” (números ficticios). Hasta Descartes los llamaba “falsas raíces”.

También recuerda que Charles Hermite fue el primero que demostró que e es un número trascendente en 1873 y fue aclamado por ello. Más tarde fue instado a demostrar que PI era también trascendente. Declinó la oferta diciendo:

No oso intentar demostrar la trascendencia de PI. Si otros emprenden esta tarea, nadie se sentirá más feliz que yo por su éxito, pero, créame, mi querido amigo, esto no puede menos que costarle un buen esfuerzo.

Fue Lindeman quien lo demostró en 1882 basándose en muchas técnicas que había introducido Hermite.

Hace una bonita biografía de Bertrand Russell y habla de mujeres matemáticas en dos capítulos de forma tan extensa que os las tendré que contar en más historias para poder sacarles todo el jugo.

Y también de los tres teoremas fundamentales en matemáticas: el de la aritmética, que dice que todo entero positivo puede ser descompuesto de forma única por factores primos; el del cálculo, que afirma que derivación e integración son operaciones inversas; y el del álgebra, que dice que cualquier ecuación polinómica de grado n escrita con números complejos tiene, precisamente, n soluciones. La demostración a este último teorema fundamental apareció en la tesis doctoral de Gauss en 1799 y se considera el mayor doctorado en matemáticas de todos los tiempos. Hay que descubrirse también ante Gauss.

Título: “El universo de las matemáticas”
Autor: William Dunham

Otras opiniones del libro:
http://deproapopa.blogspot.com/2007/10/president-of-usa.html