Historias de la Ciencia

El libro del que os quiero hablar hoy será el primero que recomiende sólo a especialistas en la materia. No obstante, he querido comentarlo porque, aunque en mi opinión sea difícil llegar a todos los conceptos de los que habla, sí he podido sacarle algunas ideas que creo que encontraréis, al menos, curiosas o entretenidas.

Imaginemos que estamos dibujando una habitación que tiene pintado en una de sus paredes un círculo y un cuadrado. Si no dibujamos esa pared de frente, el círculo se nos transformará en una elipse y el cuadrado en un trapecio. Fijaos que no se conservan distancias, ni ángulos, ni paralelismos; pero hay algo que desconcierta. Nunca veremos un círculo como un trapecio o un cuadrado como una elipse. Hay algo que se conserva. Al estudio de estas propiedades que se conservan se le llama «geometría proyectiva».

Una de las propiedades que se conserva totalmente es la colinealidad entre tres puntos. Esto es, que si una recta pasa por tres puntos en la pared, esos tres puntos proyectados, los miremos desde donde los miremos, también estarán siempre en la misma recta: en nuestro dibujo, una recta dibujada en la pared también será una recta.

El primer teórico que explicó el principio que sería la base matemática para la perspectiva fue Leon Battista Alberti. Más tarde, Piero della Francesca y Alberto Durero profundizaron en las ideas de Alberti. Los primeros hombres interesados en aplicar la geometría a la pintura fueron pintores renacentistas como Filippo Brunelleschi, Paolo Uccello y Masaccio y, a partir del año 1500, el estudio de la geometría de las proyecciones y secciones eras indispensable para todo aspirante a pintor.

He de recordaros que dos rectas paralelas en la realidad no tienen por qué serlo en un cuadro. Por ejemplo, si miramos los raíles del tren vemos que, a medida que se alejan, que cada vez están más cerca hasta que se unen en un punto. El primero en darse cuenta  que dos rectas que son paralelas en la realidad podían no serlo en un dibujo fue Gérard Desargues. Dotó a cada recta un punto en el infinito y a cada plano una recta en el infinito.

La geometría proyectiva renació en el siglo XIX gracias a varios hombres. El más curioso de ellos fue Jean-Victor Poncelet. Escribió una obra titulada Tratado de geometría descriptiva que apareció publicada en 1822, pero fue gestada entre los años 1813 y 1814, mientras su autor, oficial del ejército de Napoleón, estaba preso en Saratov. Había participado en la campaña contra Rusia y fue dado por muerto durante la retirada de Moscú. En ambientes matemáticos se oye decir con frecuencia que la geometría proyectiva moderna nació en la prisión de Saratov.

Otra cosa que desconocía (quizás no recordaba) y me ha sorprendido es el «Principio de dualidad», que es la correspondencia entre polo y polar de una cónica. Lo digo en palabras más inteligibles: Si una afirmación sobre figuras planas es cierta, e intercambiamos en ella las palabras «punto» y «recta», así como las relaciones de incidencia (punto perteneciente a una recta por recta conteniendo un punto), entonces, la nueva proposición también lo es.

Hubo, incluso, un hombre llamado Joseph Gorgone que inició la costumbre, mantenida durante muchos años, de escribir tratados de geometría a doble columna, con el enunciado dual a la derecha del original. Curiosamente, aplicando este principio al Teorema de Pascal, Brianchol descubrió un teorema: las líneas que unen los vértices opuestos de un hexágono circunscrito a una cónica pasan por un mismo punto.

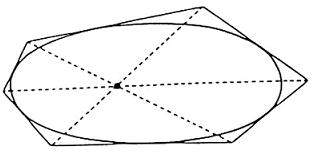
Permitidme un inciso sobre Blaise Pascal (que no consta en el libro pero sí en los enlaces que cito al final). Es el mismo gracias al cual hoy hablamos de pascales como unidad de presión, del Principio de Pascal, del triángulo de Pascal, de la apuesta de Pascal y del lenguaje de programación Pascal.

A los 11 años escribió un pequeño tratado sobre los sonidos de cuerpos en vibración. Su padre  quería que estudiara latín y griego, así que quitó todos los textos matemáticos de su casa y le prohibió continuar dedicándose a las matemáticas hasta que cumpliese 15 años. A pesar de ello, un día lo encontró escribiendo con un trozo de carbón en la pared una demostración independiente de que los ángulos de un triángulo suman dos ángulos rectos. Tenía entonces 12 años. Al verlo, su padre cambió de opinión y le permitió estudiar a Euclides y, lo que es más importante, le permitió sentarse a escuchar las asambleas de algunos de los mejores matemáticos y científicos de Europa, como Roberval, Desargues, Mydorge, Gassendi y Descartes en la celda monástica del padre Marin Mersenne.

Con 16 años escribió Essai pour les coniques que hizo llegar a Marin Mersenne. Cuando este último le enseñó a Descartes esos trabajos, se negó a creer que no fueran de su padre. Cuando todavía no tenía 19 años, y después de 3 años de trabajo, inventó la pascalina, una calculadora mecánica que utilizó la Hacienda francesa de la época. Hablo del año 1645. En los años 1960 (mñas de 300 después de su invención), IBM la utilizó internamente. Murió con tan sólo 39 años. Prometo buscar más cosas sobre Blaise Pascal y ver si algún día le podemos dedicar un artículo.

Continuemos con el libro. Jakob Steiner fue el primer matemático germano que siguió el camino iniciado por Poncelet. Llegó a hablar de cónicas de puntos y cónicas de rectas; o sea, una cónica puede ser considerada como el conjunto de sus puntos, pero también puede pensarse como la envolvente de todas sus tangentes.

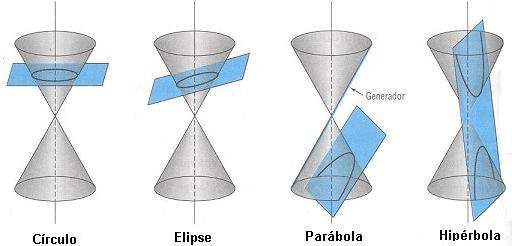
El libro habla también de las secciones cónicas, llamadas así porque salen de cortar un cono con un plano. En función del corte obtenemos las famosas elipses, parábolas e hipérbolas.

Cuando hacemos geometría proyectiva como hemos hecho hasta ahora diremos que es utilizando métodos sintéticos; pero también es posible hacer geometría proyectiva utilizando métodos analíticos. En palabras simples, cuando tratamos de puntos en el plano, ejes cartesianos y vectores.

Y, como siempre, hubo polémica entre ambos grupos de especialistas. Al principio, fue amistosa, pero pronto dejó de serlo. Los geómetras analíticos criticaban a los sintéticos por su incapacidad de demostrar el principio de dualidad en su forma más general (o sea, que la figura a la que se aplica no hace falta que sea una cónica); y los sintéticos criticaban a los analíticos la utilización del lenguaje matemático que ocultaba las ideas geométricas.

La rivalidad llegó a hacerse tan agria que Jakob Steiner, el más fanático de los sintéticos, amenazó con dejar de publicar en el Journal für Mathematik si los artículos de Plücker, el más representativo de los analíticos, seguían apareciendo allí.

Obviamente, esta discusión carece totalmente de sentido. Quizás, en cuanto a potencia de sus procedimientos, el tiempo le ha dado la razón a los analíticos, pero los métodos sintéticos, en absoluto, han dejado de utilizarse y siguen dando hermosos resultados.

El libro habla mucho, muchísimo de trucos y propiedades geométricas, de la entrada de la variable compleja en la geometría analítica; de los diferentes tipos de cúbicas, clasificadas según Isaac Newton; de la paradoja de Kramer, del teorema de Poncelet y finalmente acaba con algunas curvas conocidas (muchas de ellas suelen salir en las matemáticas de diferentes carreras técnicas y científicas) como la Leminscata de Bernoulli y otras que no conocía como la Curva del diablo, el bicornio o el astroide (si os interesa ver algunas curvas y sus fórmulas, no dejéis de ver este enlace.

Ya que hablo de curvas matemáticas, permitidme otro apunte más que no consta en el libro. La cardioide es una curva con forma de corazón. Una anécdota que me contó un compañero de facultad, es que un matemático dedicó un libro a su mujer con la dedicatoria: A mi esposa, con [y aquí puso la fórmula de  la cardioide]. Una bonita, a la vez que original dedicatoria, ¿no os parece?

Como decía al principio, el libro es bastante técnico y sólo puedo recomendarlo a quien tenga buenos o muy buenos conocimientos de geometría a niveles de la licenciatura en exactas, ingenieros, arquitectos o cualquier otra carrera donde se traten estos temas en profundidad (¿alguien me puede decir si estos temas se estudian también en la carrera de Bellas Artes?).

Si pensáis que exagero, os recomiendo echarle un buen ojo antes de comprarlo o leerlo. Ahora bien, si conocéis el tema, el libro es sensacional.

Título: «Plücker y Poncelet. Dos modos de entender la geometría»
Autor: Ricardo Moreno Castillo

(Nota: puede que tengáis problemas con los gráficos si no leéis el artículo desde el mismo blog. Ha aumentado tanto el gráfico debido al hotlinking que me he visto obligado a eliminarlo. Disculpad las molestias)

Otras fuentes:
http://suanzes.iespana.es/suanzes/pascal.htm
http://es.wikipedia.org/wiki/Blaise_Pascal